
Hôm nay chúng ta sẽ tìm hiểu về số nguyên tố - những viên gạch cơ bản của số học.
Số nguyên tố là một số tự nhiên lớn hơn 1 mà không chia hết cho số nào cả, ngoại trừ nó chia hết cho 1 và chia hết cho chính nó. Ví dụ như 2, 3, 5, 7, 11, 13 là số nguyên tố. Số 9 không phải là số nguyên tố vì nó chia hết cho 3. Số 2012 không phải là số nguyên tố vì nó chia hết cho 2.
Mỗi số tự nhiên lớn hơn 1 bất kỳ đều có thể phân tích thành tích của các số nguyên tố. Dưới đây là một vài ví dụ $$4 = 2 \times 2 = 2^2, \quad 6 = 2 \times 3, \quad 8 = 2 \times 2 \times 2 = 2^3,$$ $$9 = 3 \times 3 = 3^2, \quad 10 = 2 \times 5, \quad 12 = 2 \times 2 \times 3 = 2^2 \times 3,$$ $$2012 = 2 \times 2 \times 503 = 2^2 \times 503,$$ $$2013 = 3 \times 11 \times 61.$$ Như vậy từ các số nguyên tố chúng ta có thể xây dựng nên toàn bộ các số tự nhiên. Số nguyên tố như là những viên gạch cơ bản dùng để tạo nên tất cả các con số khác.
Chúng ta biết rằng mỗi người chúng ta có những đặc điểm và cá tính riêng biệt do chúng ta có những bộ gen khác nhau. Mỗi một số nguyên tố có thể được xem như là một gen, và từ những gen này chúng ta có thể tạo thành các số tự nhiên khác nhau.
Chúng ta biết rằng mỗi người chúng ta có những đặc điểm và cá tính riêng biệt do chúng ta có những bộ gen khác nhau. Mỗi một số nguyên tố có thể được xem như là một gen, và từ những gen này chúng ta có thể tạo thành các số tự nhiên khác nhau.
Ví dụ:
- số 4 có hai gen số 2 bởi vì $4 = 2^2$,
- số 6 có một gen số 2 và một gen số 3 bởi vì $6=2 \times3$,
- còn số 12 có hai gen số 2 và một gen số 3 bởi vì $12=2^2 \times 3$.
Tích của hai số chính là phép cọng của hai bộ gen.
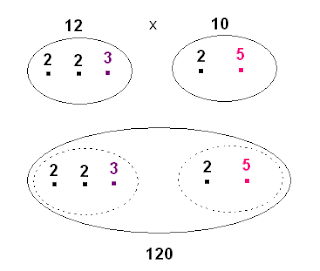
Bây giờ chúng ta xem xét về phép tính nhân. Chúng ta có $12 = 2^2 \times 3$ và $10 = 2 \times 5$. Tích của $12$ và $10$ là $120 = 2^3 \times 3 \times 5$. Số 12 có hai gen số 2 và một gen số 3. Số 10 có một gen số 2 và một gen số 5. Tích của 12 và 10 là 120 có bộ gen kết hợp của cả hai số 12 và 10, đó là ba gen số 2, một gen số 3 và một gen số 5.
Một cách tổng quát, nếu như hai số $a$ và $b$ được phân tích ra thừa số nguyên tố như sau $$a = p_1^{\alpha_1} p_2^{\alpha_2} \dots p_k^{\alpha_k}$$ $$b = p_1^{\beta_1} p_2^{\beta_2} \dots p_k^{\beta_k}$$ thì tích của chúng sẽ là $$ab = p_1^{\alpha_1 + \beta_1} p_2^{\alpha_2 + \beta_2} \dots p_k^{\alpha_k + \beta_k}.$$ Chúng ta thấy phép nhân giữa $a$ và $b$ chính là phép cọng giữa hai bộ gen của $a$ và $b$.
Tính chia hết chính là sự so sánh về hai bộ gen.
Chúng ta nói $a$ chia hết cho $b$ nếu tồn tại số tự nhiên $c$ để cho $a = bc$. Trong trường hợp này $a$ được gọi là một bội số của $b$, còn $b$ được gọi là một ước số của $a$.
Nếu hai số $a$ và $b$ được phân tích ra thừa số nguyên tố như sau $$a = p_1^{\alpha_1} p_2^{\alpha_2} \dots p_k^{\alpha_k}$$ $$b = p_1^{\beta_1} p_2^{\beta_2} \dots p_k^{\beta_k}$$ thì $a$ chia hết cho $b$ khi và chỉ khi $\alpha_1 \geq \beta_1$, $\alpha_2 \geq \beta_2$,..., $\alpha_k \geq \beta_k$. Vậy $a$ chia hết cho $b$ khi bộ gen của $a$ nhiều hơn hoặc bằng bộ gen của $b$.
 |
| 6 là ước số của 240 vì bộ gen của 6 ít hơn là bộ gen của 240 |
Ví dụ: 6 có một gen số 2 và một gen số 3, còn 240 có bốn gen số 2, một gen số 3 và một gen số 5. Cho nên 240 chia hết cho 6, 240 là bội số của 6, còn 6 là ước số của 240.
 |
| hai bộ gen của 6 và 10 không thể so sánh với nhau được |
Trong khi đó giữa hai số 6 và 10, không có số nào là ước số của số còn lại, bởi vì hai bộ gen của 6 và 10 không so sánh được. Nếu nói về gen số 2 thì 6 và 10 có cùng số lượng gen số 2. Tuy nhiên khi nói về gen số 3 thì 6 có nhiều hơn là 10, còn về gen số 5 thì 10 lại nhiều hơn là 6.
Ước số chung lớn nhất - Bội số chung nhỏ nhất
Vì $252 = 2^2 \times 3^2 \times 7$ và $120 = 2^3 \times 3 \times 5$, ước số chung lớn nhất của 252 và 120 chính là $2^2 \times 3 = 12$ và bội số chung nhỏ nhất của 252 và 120 chính là $2^3 \times 3^2 \times 5 \times 7=2520$.
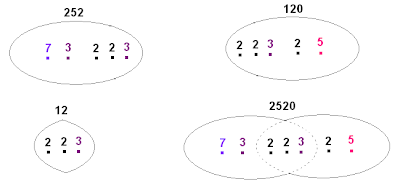
Với hình vẽ trên đây, chúng ta dễ dàng thấy rằng $$USCLN(a,b) BSCNN(a,b) = ab$$
Do đó từ bội số chung nhỏ nhất chúng ta có thể tính được ước số chung lớn nhất và ngược lại, từ ước số chung lớn nhất chúng ta có thể tính được bội số chung nhỏ nhất như sau. $$USCLN(a,b) = \frac{ab}{BSCNN(a,b)}, \quad BSCNN(a,b) = \frac{ab}{USCLN(a,b)}$$
Với $$a = p_1^{\alpha_1} p_2^{\alpha_2} \dots p_k^{\alpha_k}$$ $$b = p_1^{\beta_1} p_2^{\beta_2} \dots p_k^{\beta_k}$$ thì $$USCLN(a,b) = p_1^{\min{(\alpha_1, \beta_1)}} p_2^{\min{(\alpha_2, \beta_2)}} \dots p_k^{\min{(\alpha_k, \beta_k)}},$$ $$BSCNN(a,b) = p_1^{\max{(\alpha_1, \beta_1)}} p_2^{\max{(\alpha_2, \beta_2)}} \dots p_k^{\max{(\alpha_k, \beta_k)}}.$$ Bởi vì $\min{(\alpha_i, \beta_i)} + \max{(\alpha_i, \beta_i)} = \alpha_i + \beta_i$, chúng ta chứng minh được hằng đẳng thức $$USCLN(a,b) BSCNN(a,b) = ab.$$
Hai số nguyên tố cùng nhau có hai bộ gen hoàn toàn khác nhau
Hai số $a$ và $b$ gọi là hai số nguyên tố cùng nhau nếu ước số chung lớn nhất của chúng là 1. Từ đó suy ra chúng có hai bộ gen hoàn toàn khác nhau. Nếu $a$ và $b$ là hai số nguyên tố cùng nhau thì bội số chung nhỏ nhất của chúng chính là $ab$.
Như ví dụ dưới đây, 6 và 35 là hai số nguyên tố cùng nhau vì chúng không có gen nào giống nhau.

Hai số $a$ và $b$ gọi là hai số nguyên tố cùng nhau nếu ước số chung lớn nhất của chúng là 1. Từ đó suy ra chúng có hai bộ gen hoàn toàn khác nhau. Nếu $a$ và $b$ là hai số nguyên tố cùng nhau thì bội số chung nhỏ nhất của chúng chính là $ab$.
Như ví dụ dưới đây, 6 và 35 là hai số nguyên tố cùng nhau vì chúng không có gen nào giống nhau.

Số 1 tương ứng với bộ gen rỗng
Nếu $$a = p_1^{\alpha_1} p_2^{\alpha_2} \dots p_k^{\alpha_k}$$ thì $$a \times 1 = a = p_1^{\alpha_1} p_2^{\alpha_2} \dots p_k^{\alpha_k}$$ Do đó $$1 = p_1^0 p_2^0 \dots p_k^0$$ Vì vậy số 1 tương ứng với bộ gen rỗng.
Nếu $$a = p_1^{\alpha_1} p_2^{\alpha_2} \dots p_k^{\alpha_k}$$ thì $$a \times 1 = a = p_1^{\alpha_1} p_2^{\alpha_2} \dots p_k^{\alpha_k}$$ Do đó $$1 = p_1^0 p_2^0 \dots p_k^0$$ Vì vậy số 1 tương ứng với bộ gen rỗng.

Bộ gen của số 0 là gì?
Chúng ta dừng lại ở đây với một câu đố, đó là bộ gen của con số 0 là bộ gen gì. Bạn nào biết câu trả lời thì viết lên đây để chúng ta cùng tham khảo. Xin hẹn gặp lại các bạn ở kỳ sau.
Bài tập về nhà.
1. Chứng minh rằng ước số chung lớn nhất của hai số $a$ và $b$ cũng chính là ước số chung lớn nhất của hai số $a$ và $b-a$.
2. Chứng minh rằng nếu $ab$ chia hết cho $c$ nhưng $b$ và $c$ nguyên tố cùng nhau thì $a$ sẽ chia hết cho $c$.
3. Chứng minh rằng có vô số các số nguyên tố.
