
Tôi muốn chia xẻ với các bạn một kinh nghiệm mà tôi đã học được. Đó là khi đối diện với một bài toán mà chúng ta chưa biết phải làm như thế nào, thì việc đầu tiên chúng ta có thể làm là xem xét các trường hợp đặc biệt của bài toán. Xem xét các trường hợp đặc biệt giúp chúng ta dần dần hiểu rõ bài toán hơn. Để minh hoạ, chúng ta sẽ làm một vài bài toán.
Chúng ta đều biết rằng đi thẳng bao giờ cũng ngắn hơn là đi lòng vòng. Trong toán học, có nghĩa là nếu chúng ta có ba điểm $A$, $B$ và $C$ thì khoảng cách từ điểm $A$ đến điểm $C$ luôn luôn bé hơn hoặc bằng tổng khoảng cách từ điểm $A$ đến điểm $B$ và từ điểm $B$ đến điểm $C$. Chúng ta gọi đây là bất đẳng thức tam giác. Hôm nay chúng ta sẽ sử dụng bất đẳng thức tam giác để giải một vài bài toán hình học.
 |
| Bất đẳng thức tam giác: $AC \leq AB + BC$ |
Chúng ta làm bài đầu tiên. Trong hình dưới đây chúng ta thấy có vẻ hiển nhiên là khoảng cách từ $A \rightarrow C \rightarrow B$ sẽ ngắn hơn khoảng cách từ $A \rightarrow D \rightarrow B$ bởi vì nếu nhìn từ $AB$ thì điểm $D$ xa hơn là điểm $C$. Nhìn thì thấy hiển nhiên, nhưng cái khó là làm sao để chứng minh được nó.
 |
| có vẻ hiển nhiên rằng $AC + CB \leq AD + DB$ |
Bài toán 1. Cho hình tam giác $ABD$ và một điểm $C$ nằm trên tam giác này. Chứng minh rằng $$AC +CB \leq AD + DB.$$
Trong toán học, khi chúng ta giải một bài toán mà chúng ta chưa biết phải bắt đầu từ đâu thì việc tốt nhất là chúng ta xem xét một vài trường hợp đặc biệt. Chúng ta thử xem với những trường hợp đặc biệt đó thì bài toán có giải quyết được không. Đôi khi nhờ những trường hợp đặc biệt này mà chúng ta lại hiểu rõ hơn về bài toán. Có khi bằng cách giải các trường hợp đặc biệt mà chúng ta tìm ra được những kỹ thuật có thể dùng để giải quyết bài toán trong trường hợp tổng quát.
Trong bài toán ở trên, chúng ta thử đặt $C$ vào những vị trí đặc biệt để xem thử chúng ta có chứng minh được cái bất đẳng thức đó hay không. Chúng ta thử xem nếu $C$ nằm trên cạnh của tam giác $ADB$ thì sao.
Giả sử như $C$ nằm trên cạnh $AD$, chúng ta chứng minh $AC +CB \leq AD + DB$ được không?

Ồ, nếu như $C$ nằm trên cạnh $AD$ thì bất đẳng thức $AC +CB \leq AD + DB$ trở thành $CB \leq CD + DB$. Đây chính là bất đẳng thức tam giác. Vậy coi như chúng ta chứng minh được trường hợp này. Chúng ta cũng dễ dàng nhận thấy nếu $C$ nằm trên cạnh $DB$ thì chúng ta cũng chứng minh được.
Bây giờ quay ngược lại bài toán với điểm $C$ là một điểm bất kỳ trên tam giác $ADB$. Liệu chúng ta có thể làm cho $C$ nằm trên cạnh một tam giác nào hay không? Rõ ràng là có thể! Bằng cách kẻ đường $BC$ và cho nó cắt $AD$ tại điểm $E$ như hình dưới đây, thì điểm $C$ sẽ nằm trên cạnh của tam giác $AEB$. Vậy chúng ta có $AC+CB \leq AE+EB$. Nhưng điểm $E$ lại nằm trên $AD$, do đó chúng ta lại có $AE+EB \leq AD +DB$. Như vậy chúng ta đã giải quyết được bài toán!

Lời giải bài toán 1. Kéo dài $BC$ cho cắt $AD$ tại điểm $E$. Chúng ta có
$$AC + CB \leq AE + EC + CB = AE + EB.$$
Chúng ta lại có
$$AE+EB \leq AE + ED + DB = AD + DB.$$
Kết hợp hai bất đẳng thức lại thì chúng ta có $AC + CB \leq AD + DB. \blacksquare$
Chúng ta xem bài toán tiếp theo.
Bài toán 2. Cho hình tam giác $ABC$ và một điểm $M$ nằm trên cạnh $AC$. Chứng minh rằng tồn tại một số $0 \leq \alpha \leq 1$ để cho $$BM \leq \alpha BA + (1- \alpha) BC.$$
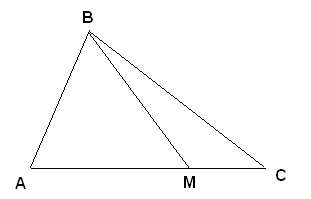
Một lần nữa, chúng ta xem xét các trường hợp đặc biệt. Nếu $M=A$ thì chúng ta cần tìm $\alpha$ để cho $BA \leq \alpha BA + (1- \alpha) BC$. Chúng ta thấy rằng trong trường hợp này $\alpha=1$ sẽ thõa mãn.
Vậy còn trường hợp $M=C$? Nếu $M=C$ thì chúng ta cần tìm $\alpha$ để cho $BC \leq \alpha BA + (1- \alpha) BC$. Trường hợp này thì $\alpha = 0$ sẽ thõa mãn.
Bây giờ chúng ta xem xét trường hợp $M$ là trung điểm của $AC$. Liệu $\alpha = \frac{1}{2}$ có thoã mãn hay không? Hay nói cách khác, liệu $BM \leq \frac{1}{2} BA + \frac{1}{2} BC$ có đúng không khi $M$ là trung điểm của $AC$? Chúng ta có thể tìm thấy một tam giác mà một cạnh bằng $BM$, cạnh khác bằng $\frac{1}{2} BA$ và cạnh còn lại bằng $\frac{1}{2} BC$ hay không?

Từ trung điểm $M$ của $AC$, nếu chúng ta kẻ đường thẳng song song với $AB$, nó sẽ cắt cạnh $BC$ tại trung điểm $N$. Chúng ta sẽ có $MN = \frac{1}{2} AB$ và $BN = \frac{1}{2} BC$. Vì vậy $BM \leq MN + BN = \frac{1}{2} AB + \frac{1}{2} BC$. Chúng ta đã giải được bài toán trong trường hợp $M$ là trung điểm của $AC$.
Bây giờ chúng ta xem xét $M$ là điểm bất kỳ trên cạnh $AC$. Liệu chúng ta có thể kẻ tam giác $BMN$ tương tự như trên được không? Nếu như từ điểm $M$ chúng ta kẻ một đường song song với $AB$ và cho nó cắt $BC$ tại điểm $N$ thì hai đoạn $MN$ và $BN$ sẽ bằng bao nhiêu? Chúng ta có $\frac{MN}{AB}= \frac{CM}{CA}$ nên $MN = \frac{CM}{CA} AB$. Chúng ta lại có $\frac{BN}{BC} = \frac{AM}{AC}$, cho nên $BN = \frac{AM}{AC} BC$. Chúng ta phát hiện ra rồi $\frac{CM}{CA} + \frac{AM}{AC} = 1$, như vậy nếu chúng ta chọn $\alpha = \frac{CM}{CA}$ thì $1-\alpha = \frac{AM}{AC}$ và chúng ta có $BM \leq MN + BN = \alpha AB + (1-\alpha) BC$. Vậy chúng ta đã giải quyết xong bài toán!

Lời giải bài toán 2. Từ điểm $M$, kẻ một đường song song với $AB$ và cho nó cắt cạnh $BC$ tại điểm $N$.
Chúng ta có $\frac{MN}{AB}= \frac{CM}{CA}$ nên $MN = \frac{CM}{CA} AB$.
Tương tự, chúng ta có $\frac{BN}{BC} = \frac{AM}{AC}$, cho nên $BN = \frac{AM}{AC} BC$.
Vì vậy $BM \leq MN + BN = \frac{CM}{CA} AB + \frac{AM}{AC} BC$.
Nếu chúng ta chọn $\alpha = \frac{CM}{CA}$ thì $0 \leq \alpha \leq 1$ và $$BM \leq \alpha BA + (1- \alpha) BC. \blacksquare$$
Đến đây chúng ta tạm dừng, hẹn đến kỳ sau chúng ta sẽ làm thêm các bài toán khác. Hôm nay chúng ta rút ra một kinh nghiệm rằng, muốn giải một bài toán thì việc đầu tiên chúng ta có thể làm là xem xét các trường hợp đặc biệt. Đôi khi giải quyết được các trường hợp đặc biệt sẽ giúp chúng ta hiểu rõ hơn bài toán và gợi ý cho chúng ta cách giải quyết bài toán trong trường hợp tổng quát.
Bài tập về nhà.

Cho tam giác $ABC$ và $DBC$. Lấy một điểm $X$ trên đoạn $AD$. Chứng minh rằng
- Diện tích tam giác $XBC$ phải nhỏ hơn hoặc bằng diện tích tam giác $ABC$ hoặc tam giác $DBC$;
- Chu vi tam giác $XBC$ phải nhỏ hơn hoặc bằng chu vi tam giác $ABC$ hoặc tam giác $DBC$.
