Giả sử trên mặt phẳng chúng ta có một điểm $P$ và một đường tròn $(O)$. Kẻ một đường thẳng qua điểm $P$ cắt đường tròn tại hai điểm $U$ và $V$. Vậy thì giá trị của $$PU \times PV$$ sẽ không phụ thuộc vào vị trí của đường thẳng.

Điều này có nghĩa là nếu chúng ta vẽ một đường thẳng khác qua $P$ và cắt đường tròn tại hai điểm $A$ và $B$ thì $$PA \times PB = PU \times PV.$$
Giá trị không đổi này được gọi là phương tích của điểm $P$ đối với đường tròn $(O)$.
Để chứng minh $PU \times PV$ không phụ thuộc vào vị trí của đường thẳng, chúng ta sẽ sử dụng tam giác đồng dạng. Chúng ta chia ra hai trường hợp: trường hợp điểm $P$ nằm bên ngoài đường tròn và trường hợp điểm $P$ nằm bên trong đường tròn.
Trường hợp điểm $P$ nằm bên ngoài đường tròn $(O)$

Chúng ta xem xét hai tam giác $PUB$ và $PAV$. Hai tam giác này đồng dạng vì có hai cặp góc bằng nhau. Cho nên $$\frac{PU}{PA} = \frac{PB}{PV}.$$
Từ đó chúng ta rút ra được điều cần chứng minh là $$PA \times PB = PU \times PV.$$
Trường hợp điểm $P$ nằm bên trong đường tròn $(O)$

Trường hợp điểm $P$ nằm bên trong đường tròn cũng vậy. Chúng ta xem xét hai tam giác $PUB$ và $PAV$. Hai tam giác này đồng dạng vì có các cặp góc bằng nhau. Suy ra $$\frac{PU}{PA} = \frac{PB}{PV}.$$
Từ đó chúng ta có giá trị của phương tích là không thay đổi $$PA \times PB = PU \times PV.$$
Tính công thức phương tích theo khoảng cách $PO$ và bán kính $r$
Bây giờ chúng ta sẽ tính công thức phương tích theo khoảng cách $PO$ và bán kính $r$ của đường tròn $(O)$. Chúng ta cũng chia ra hai trường hợp như trên: trường hợp điểm $P$ nằm bên ngoài đường tròn và trường hợp điểm $P$ nằm bên trong đường tròn.
Chúng ta sẽ chứng minh rằng:
- Nếu $P$ nằm bên ngoài đường tròn thì $$PU \times PV = PO^2 - r^2.$$
- Nếu $P$ nằm bên trong đường tròn thì $$PU \times PV = r^2 - PO^2.$$
Thật vậy, nếu chúng ta lấy $U$ và $V$ là hai giao điểm của đường thẳng $PO$ với đường tròn $(O)$ thì phương tích của $P$ sẽ được tính như sau:
- Trường hợp $P$ nằm bên ngoài đường tròn $$PU \times PV = (PO - r)(PO + r) = PO^2 - r^2.$$

- Trường hợp $P$ nằm bên trong đường tròn $$PU \times PV = (r - PO)(r + PO) = r^2 - PO^2.$$

Tóm lại công thức phương tích của $P$ có thể biểu diễn theo khoảng cách $PO$ và bán kính $r$ như sau $$PU \times PV = \pm (PO^2 - r^2).$$
Dấu cọng hay trừ trong công thức trên phụ thuộc vào vị trí của $P$ nằm bên ngoài hay bên trong đường tròn. (Trường hợp đặc biệt khi điểm $P$ nằm trên đường tròn thì phương tích hiển nhiên là bằng $0$.)
Định nghĩa "chính xác" của phương tích
Thật ra những gì chúng ta đã nói ở trên về phương tích là chưa hoàn toàn chính xác. Định nghĩa ở trên là dành cho các bạn học cấp 2 chưa học về khoảng cách có dấu, cho nên phương tích $PU \times PV$ bao giờ cũng là số dương.
Còn định nghĩa "chính xác" của phương tích là như sau $$\vec{PU} \times \vec{PV} = PO^2 - r^2.$$
Phương tích "có dấu" có thể là số dương mà cũng có thể là số âm, nó phụ thuộc vào $\vec{PU}$ và $\vec{PV}$ có cùng chiều hay ngược chiều nhau.
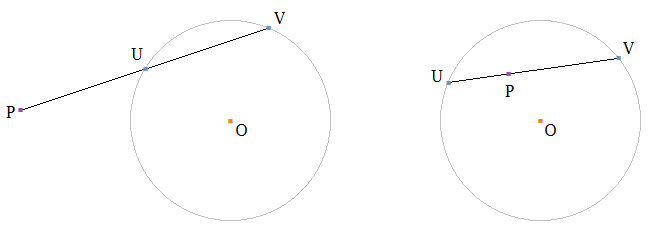 |
| Khi $P$ ở bên ngoài đường tròn thì phương tích là số dương vì $\vec{PU}$ và $\vec{PV}$ cùng chiều. Còn khi $P$ ở bên trong đường tròn thì phương tích là số âm vì $\vec{PU}$ và $\vec{PV}$ ngược chiều. |
Định nghĩa này của phương tích rất tiện lợi vì nhờ vào giá trị của phương tích mà chúng ta biết được vị trí tương đối của điểm $P$ đối với đường tròn. Nếu phương tích là số dương, chúng ta biết rằng $P$ nằm ngoài đường tròn. Nếu phương tích bằng $0$, chúng ta biết rằng $P$ nằm trên đường tròn. Còn nếu phương tích là số âm, chúng ta biết rằng $P$ nằm trong đường tròn.
Công thức hình học tọa độ của phương tích
Nếu chúng ta vẽ một hệ trục tọa độ $0xy$ thì mọi điểm $P$ trong mặt phẳng sẽ có một tọa độ $(P_x, P_y)$.

Chúng ta biết rằng công thức của đường tròn tâm $O$ bán kính $r$ là $$(x - O_x)^2 + (y - O_y)^2 - r^2 = 0.$$
Công thức phương tích chính là $$\vec{PU} \times \vec{PV} = PO^2 - r^2 = (P_x - O_x)^2 + (P_y - O_y)^2 - r^2.$$
Nhờ công thức phương tích $$(P_x - O_x)^2 + (P_y - O_y)^2 - r^2$$ chúng ta càng thấy rõ hơn vì sao giá trị của phương tích là số dương, là bằng 0, là số âm, phụ thuộc vào vị trí của điểm $P$ nằm bên ngoài, bên trên, và bên trong đường tròn.
Hôm nay, chúng ta đã học sơ qua về khái niệm phương tích. Kỳ sau, chúng ta sẽ học tiếp về một vài tính chất của phương tích.
 |
| Phương tích: $\vec{PU} \times \vec{PV} = PO^2 - r^2 = (P_x - O_x)^2 + (P_y - O_y)^2 - r^2$. |
Trước khi kết thúc, chúng ta ôn lại ba công thức cơ bản của phương tích $$\vec{PU} \times \vec{PV} = PO^2 - r^2 = (P_x - O_x)^2 + (P_y - O_y)^2 - r^2.$$
Hẹn gặp lại các bạn ở kỳ sau.
Bài tập về nhà.
1. Giả sử điểm $P$ nằm ở phía bên ngoài của đường tròn $(O)$. Vẽ đường tiếp tuyến $PT$ đến đường tròn. Sử dụng định lý Pitago để tính $$PU \times PV = PT^2 = PO^2 - r^2.$$

2. Giả sử điểm $P$ nằm ở phía bên trong của đường tròn $(O)$. Vẽ đường thẳng $UV$ vuông góc với $PO$. Sử dụng định lý Pitago để tính $$PU \times PV = PU^2 = r^2 - PO^2.$$

3. Cho hai đường tròn $(O_1)$ và $(O_2)$ cắt nhau tại hai điểm $I$ và $J$. Chứng minh rằng mọi điểm $P$ nằm trên đường thẳng $IJ$ có phương tích đến hai đường tròn $(O_1)$ và $(O_2)$ là bằng nhau.

4. Cho hai đường tròn $(O_1)$ và $(O_2)$. Tìm quỹ tích tất cả các điểm $P$ sao cho phương tích của $P$ đến hai đường tròn $(O_1)$ và $(O_2)$ là bằng nhau.
5. Cho ba đường tròn $(O_1)$, $(O_2)$ và $(O_3)$. Xác định điểm $P$ sao cho phương tích của $P$ đến ba đường tròn là bằng nhau.
